牛客对应题目链接:分割等和子集_牛客题霸_牛客网 (nowcoder.com)
力扣对应题目链接:416. 分割等和子集 - 力扣(LeetCode)

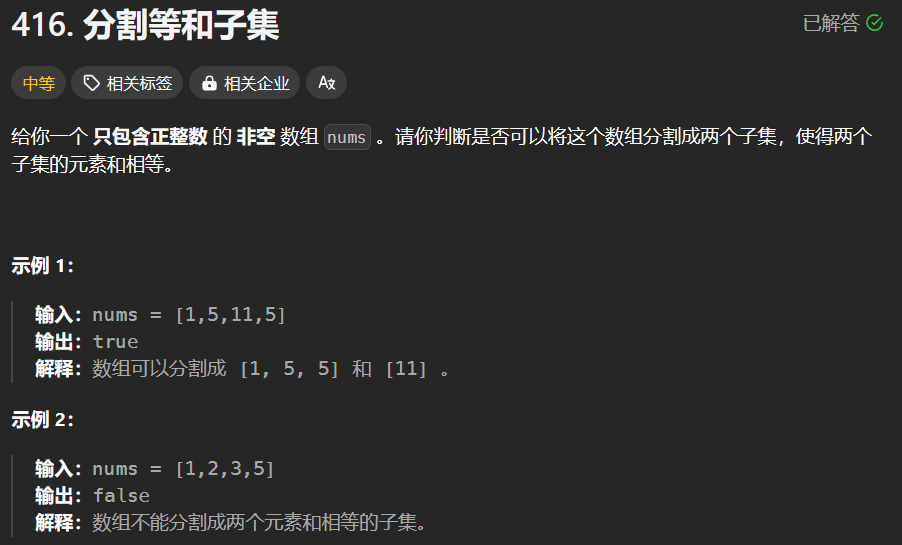
一、分析题目
01 背包 问题:将原问题转换成:从 n 个数中选,总和恰好为 sum / 2,看能否挑选出来。
- 状态 dp[i][j] 表示:从前 i 个数中挑选,总和恰好为 j,能否凑成。
- 状态转移方程:dp[i][j] = dp[i-1][j] || dp[i-1][j-arr[i]],第二个状态必须保证 j>= arr[i]
- 初始化:dp[0][0] = true
- 返回值:dp[n][sum/2]
二、代码
1、值得学习的代码
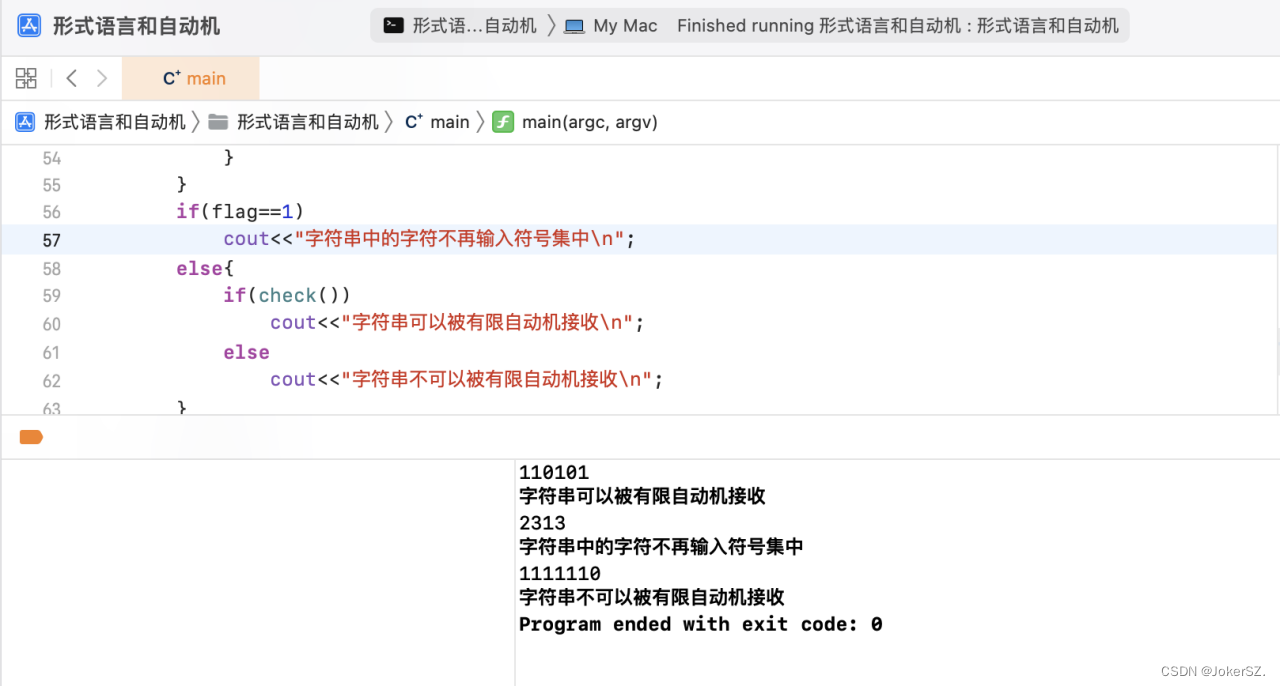
//牛客
#include <iostream>
using namespace std;
const int N = 510, M = 510 * 110 / 2;
int n;
int arr[N];
int dp[N][M];
int main()
{
cin >> n;
int sum = 0;
for(int i = 1; i <= n; i++)
{
cin >> arr[i];
sum += arr[i];
}
if(sum % 2 == 1) cout << "false" << endl;
else
{
sum /= 2;
dp[0][0] = true;
for(int i = 1; i <= n; i++)
{
for(int j = 0; j <= sum; j++)
{
dp[i][j] = dp[i - 1][j];
if(j >= arr[i])
{
dp[i][j] = dp[i][j] || dp[i - 1][j - arr[i]];
}
}
}
if(dp[n][sum]) cout << "true" << endl;
else cout << "false" << endl;
}
return 0;
}2、力扣 AC 代码(推荐)
//二维dp
class Solution {
public:
bool canPartition(vector<int>& nums) {
int n=nums.size();
int sum=0;
for(auto e:nums)
sum+=e;
if(sum%2==1)
return false;
int target=sum/2;
vector<vector<int>> dp(n, vector<int>(target+1));
for(int i=1; i<n; i++)
{
for(int j=0; j<=target; j++)
{
if(j>=nums[i])
dp[i][j]=max(dp[i-1][j], dp[i-1][j-nums[i]]+nums[i]);
else
dp[i][j]=dp[i-1][j];
if(dp[i][j]==target)
return true;
}
}
return false;
}
};
//一维dp
class Solution {
public:
bool canPartition(vector<int>& nums) {
int n=nums.size();
int sum=0;
for(auto e:nums)
sum+=e;
if(sum%2==1)
return false;
int target=sum/2;
vector<int> dp(20010);
for(int i=1; i<n; i++)
{
for(int j=target; j>=nums[i]; j--)
{
dp[j]=max(dp[j], dp[j-nums[i]]+nums[i]);
if(dp[j]==target)
return true;
}
}
return false;
}
};三、反思与改进
刚拿到这道题就直接暴力破解了,竟然还通过了 90% 的样例,导致我一度怀疑是不是有哪个特殊样例没考虑到。对数组直接进行排序,然后对总和进行判断,奇数直接 false,偶数就取总和的一般 half 作为 目标值 target,接着遍历数组进行累加,刚好等于 half 则为 true,但这样做就忽略了所选的元素可能不是连续的这一点,所以这是错的。
一般遇到这种等于 target 值的题目可以考虑背包问题。